Grafik eksponensial
Grafik Fungsi Eksponensial
Pertama, kita akan menggambar grafik fungsi eksponensial dengan melakukan plot titik-titik. Kita nanti akan melihat bahwa grafik dari fungsi semacam ini memiliki bentuk yang mudah dikenali.
Contoh 2: Grafik Fungsi Eksponensial
Gambarlah grafik masing-masing fungsi berikut.
- f(x) = 2x
- g(x) = (1/2)x
Pembahasan Tabel berikut mendaftar x mulai dari –3 sampai 3 dan nilai fungsi-fungsi f dan g yang bersesuaian dengan nilai x tersebut.

Berikut ini grafik dari fungsi-fungsi f dan g pada satu bidang koordinat.

Perhatikan bahwa

sehingga kita dapat menggambar grafik fungsi g dengan mencerminkan grafik fungsi f terhadap sumbu-y.
Gambar 2 menunjukkan grafik dari keluarga fungsi-fungsi eksponensial f(x) = ax untuk beberapa nilai basis a. Semua grafik ini melewati titik (0, 1) karena a0 = 1 untuk a ≠ 0. Kita dapat melihat dari Gambar 2 bahwa terdapat dua jenis fungsi eksponensial: Jika 0 < a < 1, fungsi eksponensial tersebut akan turun. Jika a > 1, fungsi tersebut akan naik.

Sumbu-x merupakan asimtot fungsi eksponensial f(x) = ax. Hal ini dikarenakan jika a > 1, kita mendapatkan axakan mendekati nol ketika x mendekati –∞, dan jika 0 < a < 1, kita mendapatkan ax akan mendekati 0 ketika xmendekati ∞. Selain itu, ax > 0 untuk setiap x bilangan real, sehingga fungsi f(x) = ax memiliki domain bilangan real dan range (0, ∞). Pengamatan ini dapat kita rangkum seperti berikut.
Fungsi eksponensial

memiliki domain bilangan real dan range (0, ∞). Garis y= 0 (sumbu-x) merupakan asimtot horizontal dari f. Grafik f berbentuk salah satu dari grafik-grafik pada Gambar 3 berikut ini.

Contoh 3: Mengidentifikasi Grafik Fungsi Eksponensial
Tentukan fungsi eksponensial f(x) = ax yang grafiknya diberikan oleh Gambar 4(a) dan 4(b) berikut.
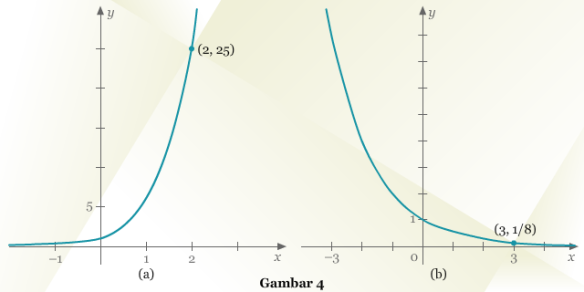
Pembahasan Pada Gambar 4(a), kita dapat melihat bahwa f(2) = a² = 25. Sehingga kita mendapatkan a = 5. Jadi, fungsi eksponensial untuk Gambar 4(a) adalah f(x) = 5x. Selanjutnya, pada Gambar 4(b) kita dapat melihat bahwa f(3) = a3 = 1/8. Sehingga a = ½. Oleh karena itu, fungsi yang memiliki grafik seperti pada Gambar 4(b) adalah f(x) = (1/2)x.
Contoh soal :
1. Lukislah grafik fungsi 𝑦 = 2𝑥 dengan 𝑥 ∈ R
Jawaban :
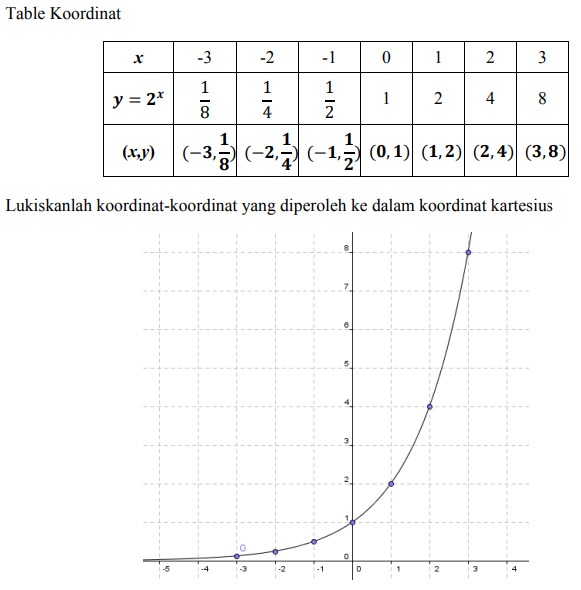

Komentar
Posting Komentar